In
the mid 1800's a British naturalist named Charles Darwin published a
book named 'The Origin of Species' and said that including human all
the living being were not put into the earth by God, rather we
evolved from other species. At that time it sounded absurd. But with
the time flow when we invented more and more new stuffs then we
gradually understood that what Darwin said was right. Overtime every
living being is evolving to keep up with the changing environment. If
it can evolve then it will survive otherwise nature will make it
vanish.
A]
Background:-
Now let us
concentrate on what Evolution is and how every living being is
evolving. Evolution is the process of change in the inherited traits
from parents over generations. Every living being gets some
traits(encoded in chromosome) from its parent and it make these
traits flow over its generation. During these flow some chromosome
combines with other type of chromosome and new types of chromosome
with new traits that belongs to neither of the participating
chromosome are evolved. This new type of chromosome may be more
superior or inferior.
pic-1
B]Why
Genetic Algorithms:-
First let me tell
you something about “hard computing” and “soft computing”.
Hard computing is the conventional computing that requires a
precisely stated analytical model and returns deterministic output.
For example ...
But soft computing
is unlike hard computing, it is tolerant of imprecision, uncertainty,
partial truth, and
approximation. In
soft computing algorithm learns to give solution. For example
Handwritten character recognition .
Genetic
algorithm(GA) is also a tool of soft computing. GA
is one of the best way to solve the type of the problem about which
very little is known. All you need to know what you need the solution
to be able to do well and GA will provide you the solution. GA is
basically a search algorithm that are applied to search for solution
in a large state space that is uneven in nature.
GA is
useful when---
=>The
search space is large and complex.
=>No
mathematical analysis is available.
=>The
problem is to find solution under multi-objective function.
=>Conventional
method fails.
C]
Basic Principles:-
GA is based on the
theory of natural selection and work on generating a set of random
solutions and making them compete in an arena where only the fittest
survives.
In GA we initially
generate a fixed number of chromosome that will form the Initial
Population. Actually each chromosome represents a possible solution
and you will ask how? This actually depends upon the programmer, how
he maps the actual problem to GA space. We need to perform this
mapping so that we can use GA operators on these chromosomes.
For example let a
maximization problem where f(x)=x^2 and x is a integer that belongs
to [0,31]. Here we can represent the possible values i.e integer
decimal values into string of binary numbers of length 5. Our Initial
population may contain chromosomes
10001(17),01010(10),11001(26),10100(20).
Then we will
select chromosomes with some selection procedure that will go to
matting pool where all GA operators will be applied . In matting pool
chromosomes are selected in pairs and crossover operator is applied
on them and similarly mutation operator is also applied on them. This
process will continue until a termination condition arises. After the
completion of the algorithm there is a high chance that we will get a
feasible solution. Yes there is also a fitness measuring function
that will keep track of the fitness of each chromosome, at the time
of crossover we will replace some chromosome with least fitness,
following the theory of 'Survival of the fittest'.Actually generally
selection process and termination condition is dependent on this
Fitness function. Thus starting from a set of random solutions the
algorithm uses these operators and fitness function to guide its
search for the optimal solution.
D]
Methodology:-
1]Initialization:-
To start GA first we need to
define the Maximum allowable population(number of maximum
chromosome), Maximum number of generation we will allow the algorithm
to generate . We also need to define the crossover rate and mutation
rate these two value will specify whether a particular chromosome
will undergo crossover and mutation. Above all we need to generate
the initial chromosomes with which we will start our selection
procedure. We can apply some logic to assign the values of the
chromosomes or simply can randomly assign values to chromosomes.
For example for
above described problem we can generate chromosome using only two
constraint one is that chromosome will contain only binary values and
chromosome will be of length 5. Then we can generate chromosomes of
length 5 up to Number of initial population.
2]Calculate
Fitness: GA generates solution based on the
fitness value of a chromosome. So after initialization we need to
calculate the fitness value of each of the chromosome in the
population. We will calculate the fitness value using a Objective
function that is called a Fitness function.
2.1]
Fitness function: A fitness function is a
particular type of objective function that is used to evaluate the
quality of a chromosome. It assigns a fitness value to all the
chromosome in the population. This function will vary according to
the problem. Fitness function should contain all the variables that
affects the solution. For some constraint satisfaction problem there
will be some constraints that will lead the search. Of course these
constraint will have different effect on the solution. Some will have
much effect and other will have less. So we need to assign some sort
of weight to these constraint according to their effect on the
solution. For example ,in a constraint satisfaction problem we can
define a fitness function as f(X)= ((CS*X)-((N-X)*CNS))/(CS*N) where
CS is cost for satisfying a constraint and CNS is cost for not
satisfying a constraint. N is the total constraint applied on the
problem and X is the number of satisfied constraint.
3]Selection:-
GA use the selection operator
to select chromosome from the population that will go to matting pool
and various GA operator will be applied on them. As the selected
chromosomes are the ones whose genes are inherited by the next
generation, it is desirable that the selected chromosomes will have
good fitness value. The convergence rate of a GA is highly determined
by the selection method, with better selection process resulting in
higher convergence rates. However, if the selection process is not
good enough, the convergence rate will be slow. If the selection
process is too active then it may create problem by converging to an
sub-optimal solution.
3.1] Roulette Wheel
Selection:- Roulette
Wheel selection
This can be simulated by following algorithm.
1.Calculate sum of all chromosome fitness(S) in population.
2.Generate random number (r) from interval (0,S).
3.Go through the population and sum fitness from first chromosome. When the sum is greater than r , stop and return the chromosome where you are.
pic-2
3.2] Tournament
selection:- It is also one of the popular method for
selection procedure. In this method we first set a value for the size
of tournament let it be k. Then we select k chromosomes randomly from
the population. Now we have (n/k) number of sets each containing k
chromosomes. Now select the chromosome with best fitness value from
each set. Thus we can select n/k number of chromosomes which will go
to matting pool.
For example let the population contains 4 chromosome aschromosome no. Fitness value
1 2
2 1
3 4
4 3
Now let k=2 and we combine chromosome 1 and 2 in a set and 3 and 4 in other. From first set chromosome 1 will be selected and from second set chromosome 3 will be selected. Total 4/2=2 chromosome will be selected for matting pool.
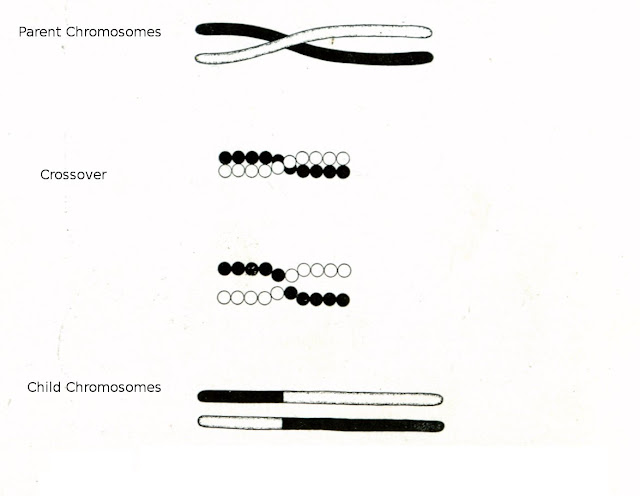
4]Crossover:- It is performed on selected chromosomes to generate offspring. The idea behind crossover is that the offspring may inherit the good traits from its parent and a better chromosome will evolve. Thus GA offers an opportunity to share better solution from one to another.
First we need to find the chromosomes from matting pool that will undergo crossover using crossover rate. Crossover rate specifies the number of chromosomes that will undergo the crossover operation. It will be in the range [0,1]. To select chromosome from matting pool we will generate a random number “r” with value [0,1], if “r” is less than the Crossover rate then that chromosome will undergo crossover. Thus total chromosome that will undergo crossover operation is Total population * Crossover rate.
Then Crossover operator operates on
the selected chromosomes in the following way..
[1]Choose a random
point on the two parents
[2]Split parents
at this crossover point
[3]Create children
by exchanging tails
Crossover may be
of various type like
Single Point :-
In this case we randomly select a crossover point then swaps the
contents of the parent chromosomes. For example, let crossover point
be 5
Parent
chromosome Child
chromosome
1278734919 1278747933
8911947933 8911934919
Two Point:- In
this case we randomly selects two crossover point and then swaps the
contents of the parent chromosomes. For the below example let the
crossover points be 3 and 7
Parent
chromosome Child
chromosome
1278734919
1271947919
8911947933 8918734933
Uniform Point:- bits are copied
from the first or from the second parent depending upon the mask
value ( 0 and 1 )that is generated randomly equal to the number of
bits in the chromosome. For example let the mask be 1100100110 (let 0
means copy from first parent to first child and 0 means copy from
second parent to first child).
Parent
chromosome Child
chromosome
1278734919
1211747913
8911947933 8978934939
5]
Mutation :- During
the execution algorithm may stuck into a local optima that is
obviously not our required solution. To get rid of these situation we
can use the mutation operator. It
is the operator that
operated upon the selected chromosome. Mutation randomly selects some
mutation points and inverts the contents of those points. Thus
mutation enables GA to jump to a random area in the solution space.
The positions where mutation is taking place is called Mutation
point. We will use Mutation operator to select the bits of chromosome
where the mutation will take place. We can write algorithm for
mutation operator as:
- For each chromosome (C) in matting pool
- For each bit in (C)
- generate a random number “r” in[0,1]
- if r<MUTATION_RATE then invert the bit
Here the total
number of bits that will undergo mutation is equals to Number of
chromosomes in matting pool * chromosome length * MUTATION RATE .
For example let
there are two chromosomes (each of them of length 5) in matting pool
and let the MUTATION_RATE=0.4
10101 and 01010.
Now generate (5*2)=10 random numbers in[0,1] say,
0.1,0.5,0.3,0,7,0,3(for first chromosome ) and 0.6,0,35,0,24,0.9,0.12
(for second chromosome )
so
for first chromosome 2nd
and 4th
bits will be inverted and for second chromosome 1st
and 4th
bits will be inverted. So the resultant chromosomes are: 11111
and 11000.
6] Termination:-
Evolution in the real
world of nature , is a continuous process. In the world of computing
“how long do we need to continue the GA to get a feasible
solution?” is a problem to be sorted out. In most of the problem we
do not know the best value of the fitness function. We therefore stop
the search when we feel that there has not been an improvement in
either the maximum or average fitness of the population over several
generations. The GA is then said to have done its work though here
is never a guarantee that the global optimum has been reached.
The algorithm may
take very long time to converge to a particular result where it may
provide a solution that is acceptable. In that case algorithm will
not stop unless we forcefully stop it. In that case we need to define
the termination condition other than getting a actual solution like
Acceptable error. Maximum allowable population may also be a
termination criteria as we GA sometime requires an enormous amount of
memory.
E]Flowchart:-
We
can represent the whole idea of GA in a flowchart form as:
pic-3
F]Application:-
Some of the fields where GA can be used are
DOMAINS APPLICATION
Machine learning designing neural networks,
classification algorithms
Signal Processing filter design
Scheduling manufacturing, resource allocation
Game playing poker,checker,Prisoner's dilemma
Optimization traveling salesman, bin
packing, graph coloring
Robotics trajectory planning
Control missile evasion, pole balancing
G]Example:- To show the use of GA I have used the Six-hump Camel Back function. I will try to find the global minima of this function using GA. This function have total six minima, two of them are global. The function is:

This is the 3-D plot of the function:
and this is the contour plot of the function showing 4 local minima and 2 global minima:
I will use a package "genalg" in language R in this purpose. This package provides a function "rbga" to implement floating point GA. This function requires a user specified evaluation function. Here is my evaluation function:
evaluate_shortest_path<-function(string=c())
{
returnValue <- (4-(2.1*string[1]^2)+(string[1]^4/3)) * string[1]^2 + (string[1] * string[2] ) + ( -4 + (4 * string[2]^2)) * string[2]^2;
returnValue
}
and here is the function call to GA:
rbga.results=rbga(c(-1.9,-1.1),c(1.9,1.1),monitorFunc=NULL,evalFunc=evaluate_shortest_path,
mutationChance=0.1,popSize=50,iters=2000)
and result can be checked as:
summary (rbga.results, T)
GA SettingsThis result is close to one of the global minima: x1=-0.089842, x2=0.712656.
Type = floats chromosome
Population size = 50
Number of Generations = 2000
Elitism = 10
Mutation Chance = 0.1
Search Domain
Var 1 = [-1.9,1.9]
Var 2 = [-1.1,1.1]
GA Results
Best Solution : -0.0899352302238796 0.712727474793792
H]References:-
[2] “Genetic Algorithms in search, Optimization and
Machine Learning” by David E. Goldberg
[3] “Neural Networks,Fuzzy Logic and Genetic
Algorithms--synthesis and applications” by S.Rajasekaran and G.A.
Vijayalakshmi Pai.




No comments:
Post a Comment